Preprocessing
For the preprocessesing steps I checkout the columns of the dataset
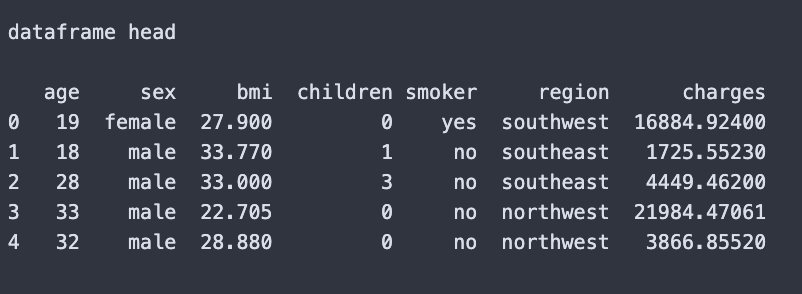
I then ensured there were no nulls in the dataset
The libraries I used below:

Hello everyone, for this project I chose to work with the Medical Insurance Cost Dataset by Mosap Abdel-Ghany. My main goal was to explore whether classification models could help uncover patterns in medical charges. Specifically, I wanted to investigate the relationship between smoking and insurance costs, and determine whether smokers in the dataset tend to have higher charges on average.
This problem is important because healthcare costs are a major concern both for individuals and for the system as a whole. By understanding which factors contribute most strongly to higher charges, we can gain insights into health behaviors and risk. Decision trees offered a practical way to approach this question, since they not only provide predictions but also show how variables like smoking status, BMI, age, and charges interact in a transparent and interpretable way.
The dataset has one file called insurance.csv, it has 7 columns(age,sex,bmi,children,smoker,region,charges). It has a usability score of 10.0 (very little to no nulls in the values). It has insurance cost for 1338 individuals. The target variable is charges(represents the the medical insurance cost billed to the individual).
For the preprocessesing steps I checkout the columns of the dataset

I then ensured there were no nulls in the dataset

The libraries I used below:


Placeholder text for analysis.
Here are some graphs for Charges vs Age and Charges vs BMI(smoking vs non-smoking)
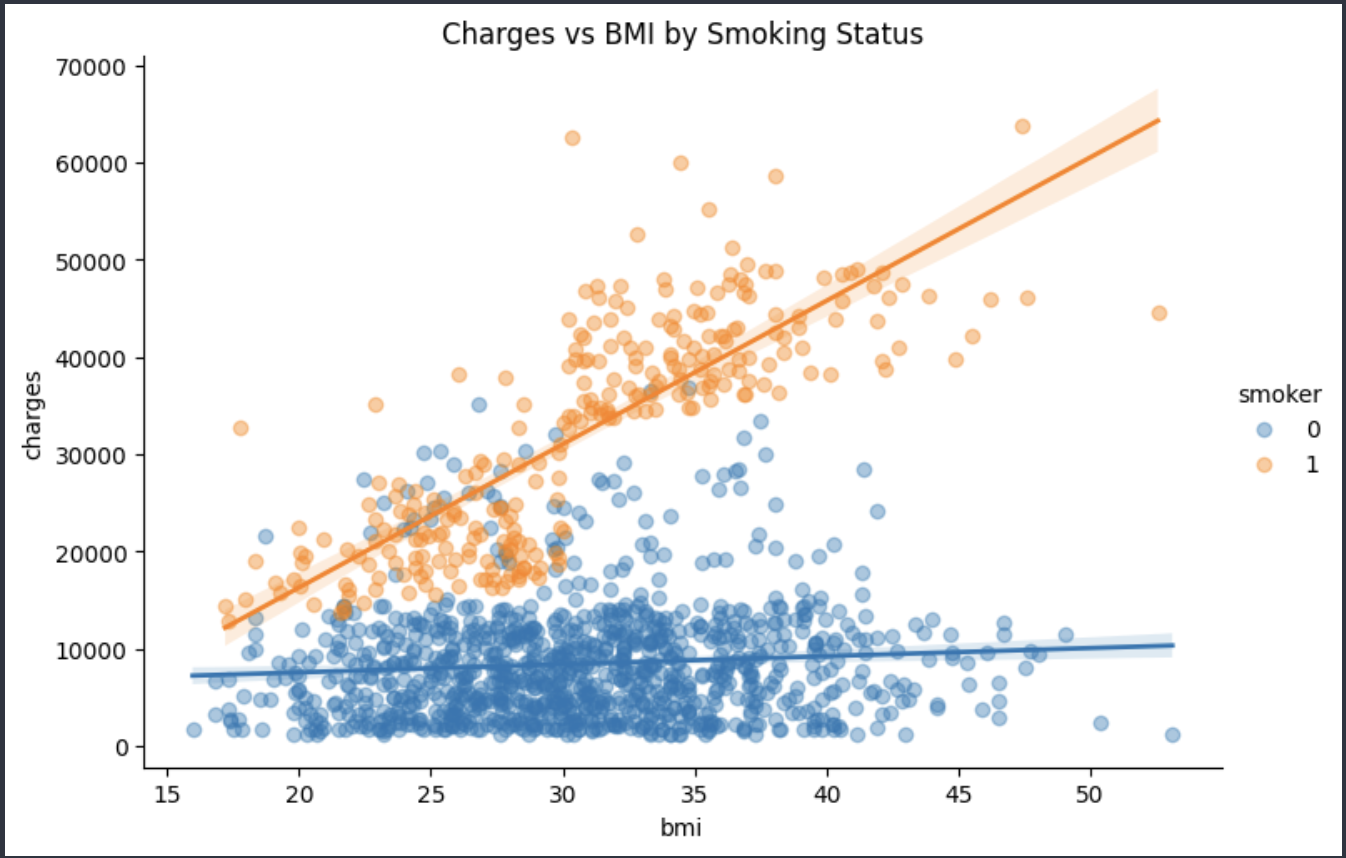
For the charges vs bmi graph in relation to smokers, it showed that charges don't rise up dramatically for non-smokers with BMI. For smokers on the other end the line is much higher compared to the latter, and therefore suggests that BMI itself isn't too much of a factor when it comes to charges, but smoking itself is the major cost driving factor.
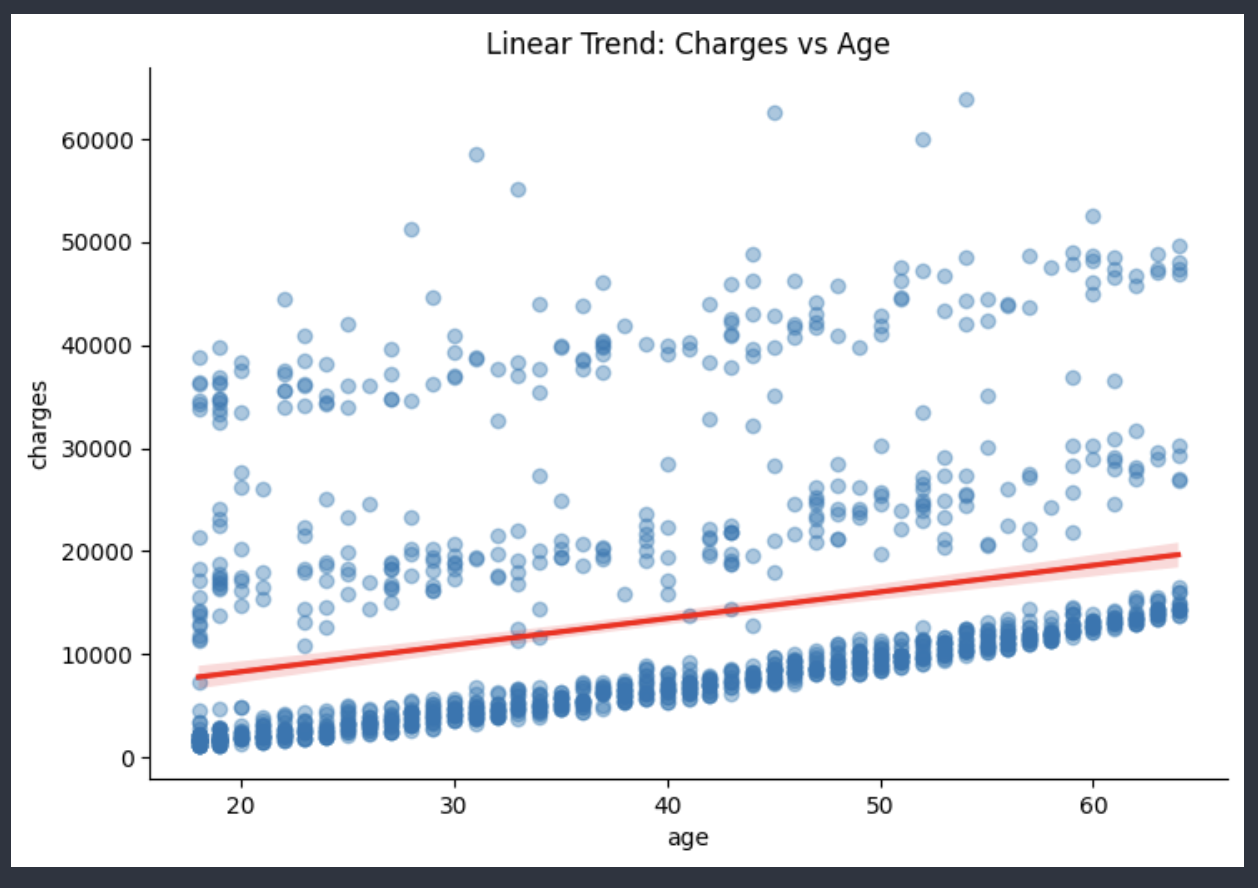
For the Charges vs Age graph it generally showed that medical charges seem to increase with age. Younger people having less medical costs, Older people having a wide array of costs typically all leading towards the increased costs area. Age is related to more increased health risks, so this checks out that insurers will charge more as people age. It's not a perfectly linear trend however there are indications for upward trends as shown in the graph
BMI itself doesn't impact the charges in a meaningful or correlating way, however BMI with Smoking does tend to see higher insurance prices than just BMI alone.
I decided on using Decision Trees as they were pretty straightforward and the best choice for the dataset I selected. Decision Trees make decisions by mapping out different choices and their possible outcomes. They are commonly used in machine learning for problems like classification and prediction.
I also needed to prepare the dataset and split it into training and testing sets, which is a necessary step for classification problems. I developed several helper functions to simplify the code. These included: splitdataset(), train_using_gini(), train_using_entropy(), prediction(), cal_accuracy(), and plot_decision_tree().
splitdataset() — This function splits the dataset into training and testing sets. The model learns patterns from the training set and is then tested on unseen data (testing set). This process helps the model build rules and optimize its ability to generalize to new data.
train_using_gini() — This function trains a decision tree using the Gini Index as its criterion for splitting. The Gini Index measures how “pure” a node is (whether it mostly contains one class). A lower Gini value means better splits (clearer separation, in this case, between smokers and non-smokers).
train_using_entropy() — This function is similar to train_using_gini() but uses entropy instead. Entropy measures the amount of disorder or uncertainty in the dataset. The goal is to reduce entropy with each split in the tree.
prediction() — This function takes the test data and uses the trained model to make predictions (e.g., whether someone is a smoker or not). It then outputs the predicted values.
cal_accuracy() — This function evaluates how accurate the predictions were. It generates a confusion matrix (a table showing correct and incorrect predictions), calculates the accuracy score (the percentage of correct predictions), and produces a classification report (precision, recall, and F1-score). Together, these metrics give a full picture of the model’s performance.
plot_decision_tree() — This function creates a visualization of the decision tree. It displays the splits, thresholds, and decision paths used by the model.
I used a decision tree as it perfectly can handle numerical and categorical data, and effective for classification problems in general.Decision Trees are effectie for solving the problem I had of predicting smoking status.
I split the dataset into training and testing, which is standard for Classification. It was done via the helper functions I developed. The model learns from one portion of the data, which then gets tested on unseen data to check if its findings generalizes well. During training the Decision Tree will create rules and splits in the dataset to minimize node impurities, while testing how accurate these rules are.
Some of the evaluation metrics I used were precision, recall, f1-score, and accuracy.
The Gini-based decision tree achieved an accuracy of 95.76%, which indicates that the model performs very well. For precision, I got 0.98 for class 0 and 0.93 for class 1. Recall was 0.97 for class 0 and 0.92 for class 1. The F1-score was 0.98 for class 0 and 0.92 for class 1.
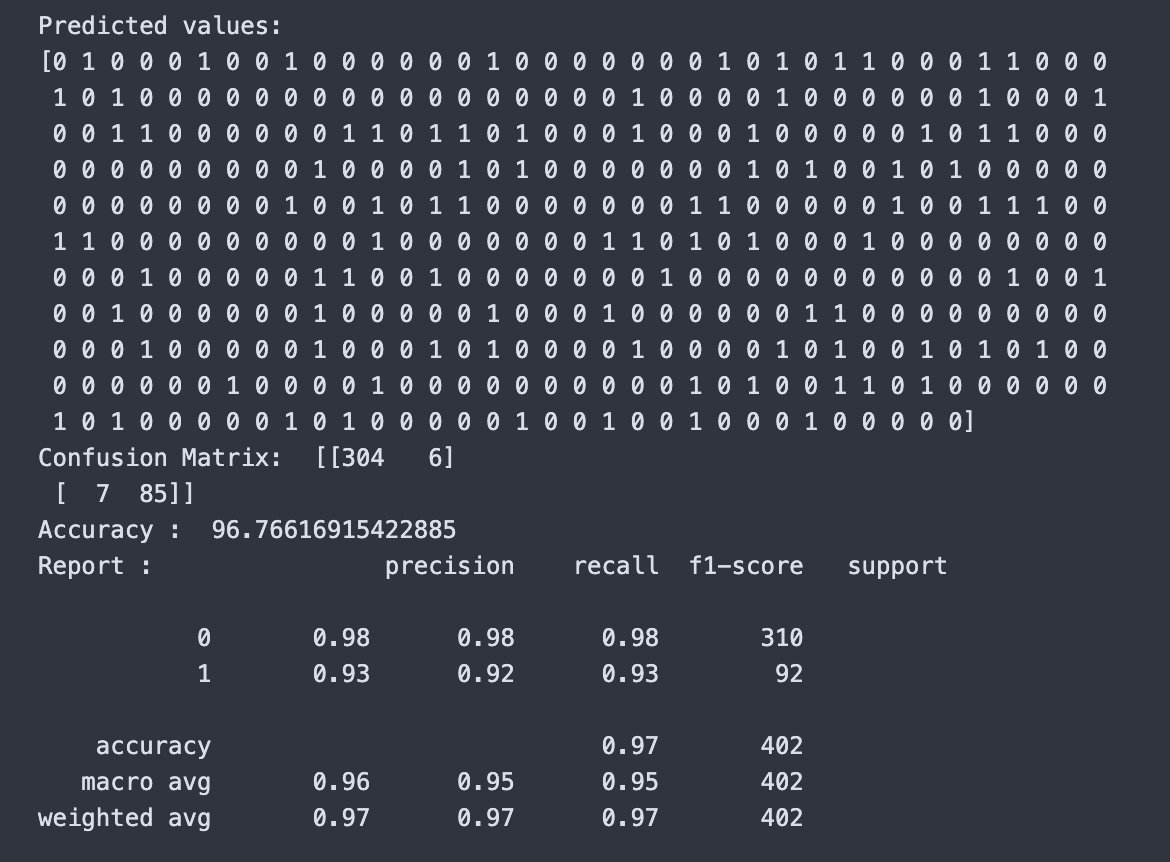
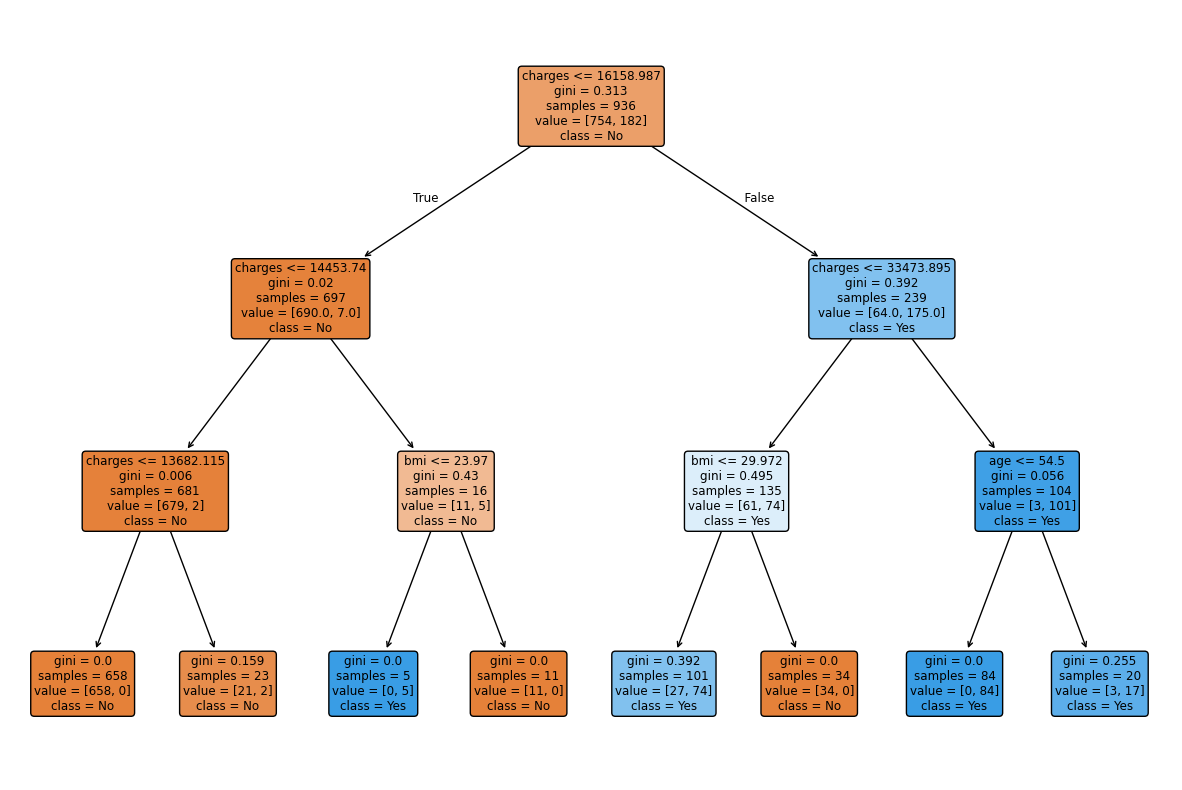
The Entropy-based decision tree achieved an accuracy of 97.26%, which is slightly higher than the Gini model. For precision, I got 0.98 for class 0 and 0.94 for class 1. Recall was 0.98 for class 0 and 0.94 for class 1. The F1-score was 0.98 for class 0 and 0.94 for class 1.
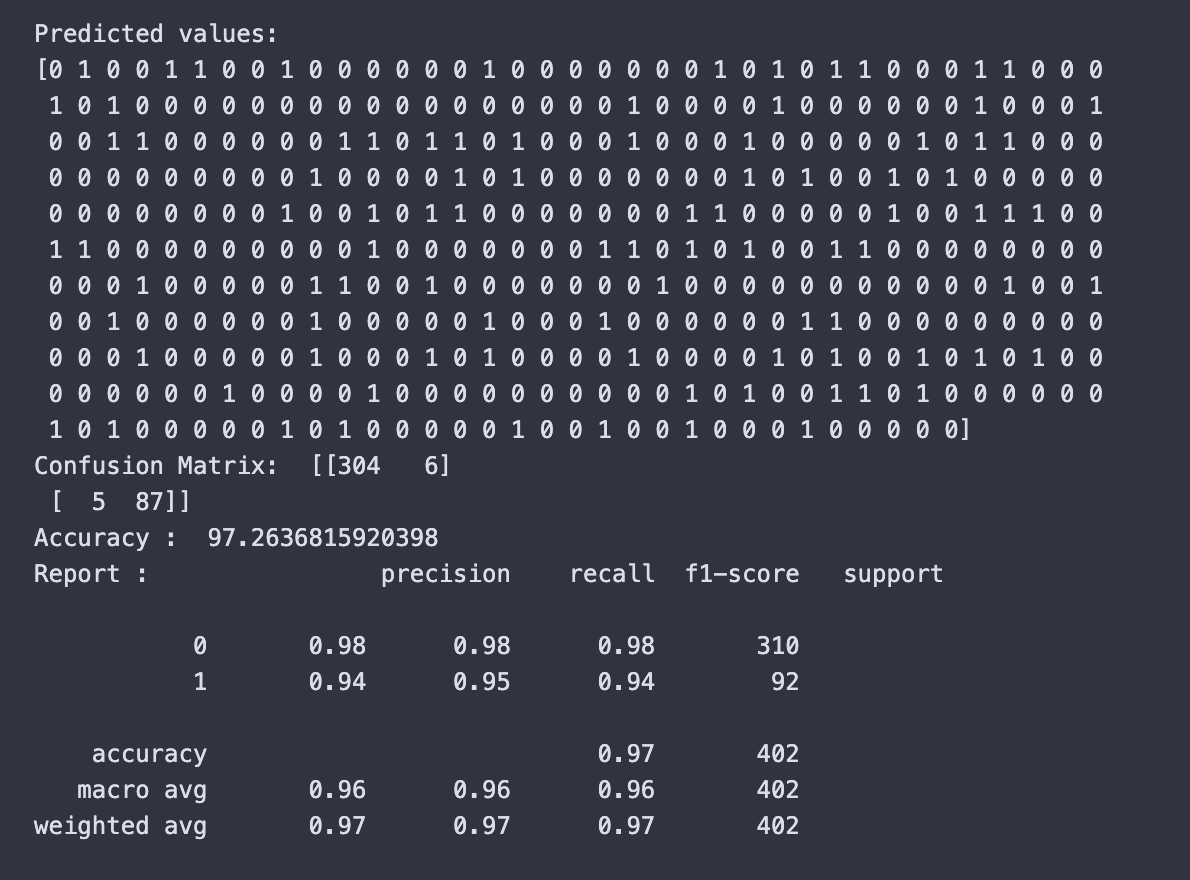
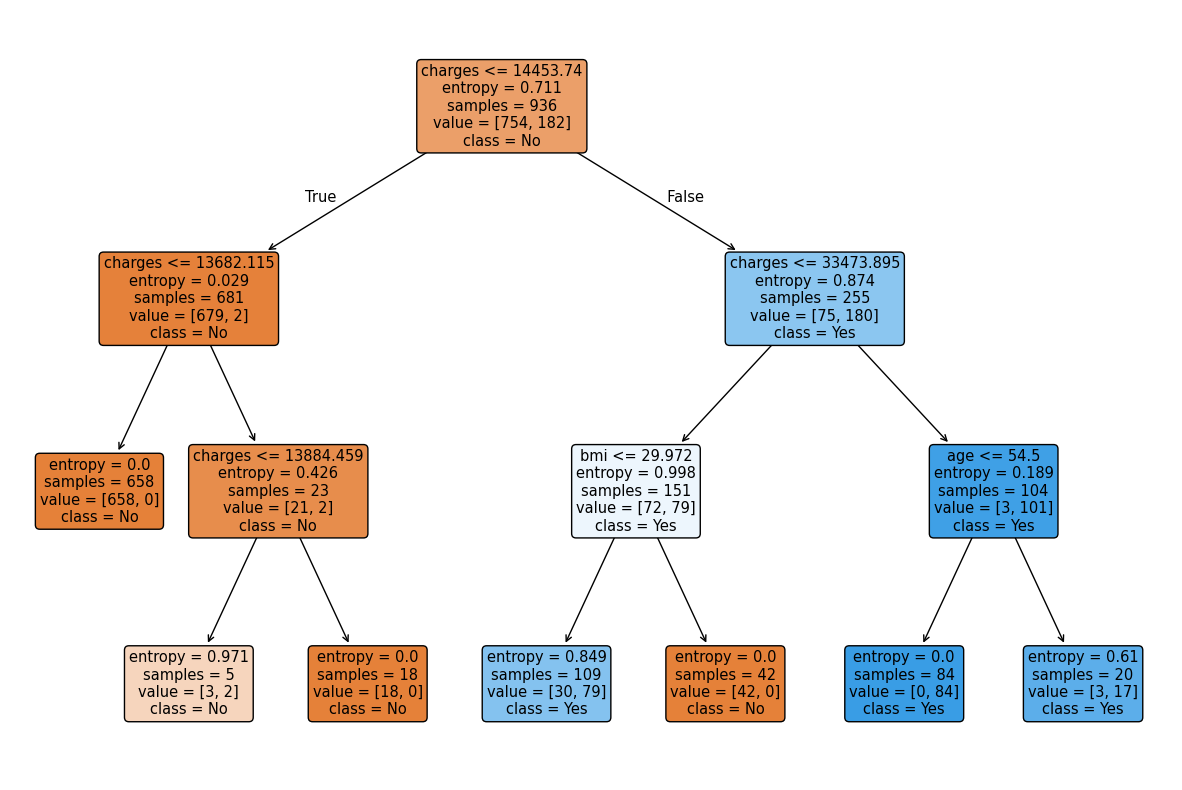
Both models performed strongly, but entropy provided a modest improvement in overall accuracy and better balance between precision and recall for the minority class. The decision tree visualizations confirm that charges is the most important predictor, followed by bmi and age.
When I began this project, my main question was whether decision trees could effectively classify outcomes in this dataset, and whether Gini or Entropy would serve as the better criterion.
After training both models, I found that each performed strongly, but with some differences. The Gini-based model achieved an accuracy of 95.76%, while the Entropy-based model improved slightly to 97.26%. This showed me that even subtle changes in the way splits are calculated can affect overall performance.
One of the most valuable insights was identifying which features mattered most. In both models, charges consistently appeared at the root of the decision tree, making it the most important predictor. Secondary factors like bmi and age refined the classifications further, but it was charges that carried the most weight.
I also noticed that the Entropy model handled the minority class more effectively. Its improvements in precision, recall, and F1-score for that group suggested that it provided a fairer balance across the categories.
In the end, I was able to answer my initial question. Decision trees not only modeled the dataset accurately, but the Entropy-based tree offered a small but meaningful advantage. This process gave me a clearer understanding of the data itself, as well as the strengths of different modeling approaches.
Projects like this highlight the potential for data-driven models to improve decision-making in areas such as healthcare and insurance. By identifying which factors are most influential, models can help organizations make more informed choices and even design policies that reflect real-world trends. For example, if charges are strongly tied to outcomes, that insight could be used to anticipate patient costs or allocate resources more efficiently.
At the same time, it is important to recognize possible ethical implications. Decision trees, while transparent compared to other machine learning methods, still rely heavily on the data they are trained on. If that data contains biases, the model may unintentionally reinforce them. For instance, using features such as age or BMI could create unfair disadvantages for certain groups if the results were applied without careful oversight.
Socially, the impact of such models can be positive when they are used to increase access, reduce costs, or identify risks earlier. However, there is also a risk of misuse if the predictions are applied in ways that prioritize profit over fairness or patient well-being. The key lesson is that while the technology is powerful, its impact ultimately depends on the values and goals of those who implement it.
That said, I am not a professional data scientist. I am a Computer Science student at UNC Charlotte, and these conclusions are drawn from an academic perspective. They should be interpreted accordingly and not regarded as expert findings.
consulted with chatgpt over figuring out which model to use